1 Background
Tendermint is a server and a protocol for building linearizable (or sequentially consistent) byzantine fault-tolerant applications. Tendermint validators accept transactions from clients over HTTP, and replicate them to the other validators in the cluster, forming a totally ordered sequence of transactions. Each transaction is verified by a cryptographic signature over the previous transaction, forming a blockchain. As long as more than 2/3 of the cluster is online, connected to each other, and non-malicious, progress and linearizability of transactions is guaranteed. In the presence of byzantine validators which control 1/3 or more of the voting power, safety is no longer guaranteed: the cluster may exhibit split brain behavior, discard committed transactions, etc.
Transactions are first broadcast, via a gossip protocol, to every node. A proposer, chosen by a deterministic round-robin algorithm, bundles up pending transactions into a block, and proposes that block to the cluster. Nodes then pre-vote on whether they consider the block acceptable, and broadcast their decision. Once a 2/3 majority pre-vote yes, nodes pre-commit the block, and broadcast their intention to commit. Once 2/3 of the cluster has pre-committed a block, the block can be considered committed, and the initiating node can learn the transaction is complete. Tendermint therefore requires four network hops to complete a transaction, given a totally-connected non-faulty component of the cluster holding more than 2/3 of the total votes.1
Proposers create and propose new blocks roughly once a second, though this behavior is configurable. This adds about 500 ms of latency to any given transaction.2 However, because a block encompasses multiple transactions, transaction throughput is not limited by this latency, so long as transactions can commit regardless of order. Where one transaction depends on another—for instance, when multiple actors concurrently update a record using a [read, compare-and-set] cycle, throughput is inversely proportional to network latency plus proposer block delay.
Like Bitcoin and Ethereum, Tendermint is a blockchain system. However, where Bitcoin defines a currency, and Ethereum defines a virtual machine for computation, Tendermint deals in opaque transactional payloads. As in Raft, the semantics of those transactions are defined by a pluggable state machine, which talks to Tendermint using a protocol called the ABCI, or Application BlockChain Interface.3 There are therefore two distinct programs running on a typical Tendermint node: the Tendermint validator, and the state machine application. The two communicate via ABCI over a socket.
There are several ABCI applications for use with Tendermint, including Ethermint, an implementation of Ethereum; Basecoin, an extensible proof-of-stake cryptocurrency, and Merkleeyes, a key-value store supporting linearizable reads, writes, and compare-and-set operations, plus a weaker, sequentially consistent read of any node’s local state. In these tests, we’ll use Merkleeyes to evaluate the combined safety properties of Tendermint and Merkleeyes together; we have not evaluated Ethermint or Basecoin.
2 Test Design
We model Merkleeyes as a linearizable key-value store supporting single-key reads, writes, and compare-and-set operations, and use the Jepsen testing library to check whether these operations are safe. Jepsen submits transactions via Tendermint’s HTTP interface, using /broadcast_tx_commit to block until the transaction can be confirmed or rejected. Jepsen then verifies whether the history of transactions was linearizable, once the test is complete.
We introduced three modifications to Merkleyes to support this test. Originally, users queried Merkleeyes by performing a local read on any node, instead of going through consensus. This allowed stale reads, so the Tendermint team added support for read transactions, which should be fully linearizable.
In addition, one cannot execute the same transaction more than once in Tendermint: two transactions with the same byte representation—say, “write meow to key cat”—are considered to be the same transaction. Tendermint’s maintainers added a 12-byte random nonce field to the start of Merkleeyes transactions, which lets us perform the same operation more than once.
Early experiments also led to crashes and storage corruption in Merkleeyes, which the Tendermint team traced to a race condition in check_tx, where rapid mutation of the on-disk tree representing the current data store could lead to premature garbage collection of a tree node which was still in use by the most recent version of the tree. While a full fix was not available during our tests, Tendermint provided Jepsen with a Merkleeyes build patched to work around the issue.
2.1 Compare-and-set Registers
We designed two tests for Tendermint. The first, cas-register, performs a randomized mix of reads, writes, and compare-and-set operations against a small pool of keys, rotating through keys over time. We verify the correctness of these operations using the Knossos linearizability checker. To improve per-operation latency at the cost of throughput, we lower or altogether skip the commit timeout, putting transactions through consensus immediately instead of waiting to batch them together.
Unlike many quorum or leader-based distributed systems, Tendermint nodes have no notion of “the system is down”, and will never reject a transaction for want of available replicas. This is partly a consequence of its leaderless design: nodes have no way to recognize that they are, for instance, followers who cannot execute a transaction. This also stems from Tendermint’s aggressive use of asynchronous gossip for state exchange: even if a node cannot directly replicate a transaction to a 2/3 majority of peers, it may be able to reach one peer who can re-broadcast the transaction to a majority eventually.
This makes verifying Tendermint somewhat difficult: when the network is partitioned, in-flight requests will hang for a significant amount of time—potentially the duration of the partition. Moreover, these indefinite latencies persist so long as the system is degraded, instead of being a transient phenomenon. Jepsen needs to keep performing requests, so after a timeout, we declare those operations indeterminate and perform new ones. Whether we perform timeouts or not, this introduces large windows of concurrency for transactions, which has two consequences: first, it increases the state space for the linearizability checker, leading to slow and potentially impossible-to-analyze histories, and second, it increases the number of legal states at any given point, which prevents us from catching anomalies—cases where the system reached an illegal state.
To address the performance problem, we added a new algorithm to Knossos, based on Lowe, Horn and Kroening’s refinement of Wing & Gong’s algorithm for verifying linearizability. Following Lowe’s approach, we apply both Lowe’s just-in-time graph search (already a part of Knossos) and Wing & Gong’s backtracking search in parallel, and use whichever strategy terminates first. This led to dramatic speedups—two orders of magnitude—in verifying Tendermint histories.
However, the indeterminacy problem is not a performance issue, but rather an inherent consequence of our test design. To keep state spaces small, Jepsen linearizability tests typically use reads, writes, and compare-and-set over a small space of values: for instance, the integers {1, 2, 3, 4, 5}. We detect nonlinearizable histories by observing an impossible operation, like “read 3” when the set of legal values, at that point in the history, was only {1, 2}. When there are many concurrent writes, we saturate the state space: more and more values are legal, and fewer and fewer reads are illegal. It becomes harder and harder to detect errors as the test goes on and more operations time out.
We need a complementary approach.
2.2 Sets
In addition to the cas-register test, we have a second test which uses a single key in Merkleeyes to store a set of values. Each client tries to add a unique number i to this set, by reading the current set S, and performing a compare-and-set from S → (S ∪ {i}). At the end of the test, we read the current key from Merkleeyes and identify which numbers were preserved.
If the system is linearizable, every prior add operation should be present in the read set; we can verify this in O(n) time, instead of solving the NP-hard problem of generalized linearizability verification. Moreover, crashed operations have no effect on the safety of other, concurrent operations; we don’t have to worry about the state space saturation problem that limits the linearizable register test. On the other hand, we cannot detect transient errors during the test; the system is free, for instance, to be sequentially or even eventually consistent, so long as all successful adds appear in time for the final read(s).
3 Failure Modes
While running these test workloads, we introduce a number of faults into the cluster, ranging from clock skews, crashes, and partitions, to byzantine faults like duplicate validators with partitions, write-ahead-log truncation, and dynamic reconfiguration of cluster membership.
3.1 Clocks
Tendermint uses timeouts to trigger fault detection and new block proposals. We interfere with those timeouts through a randomized mixture of long-lasting clock offsets and high-frequency clock strobing, intended to create both subtle and large difference between node clocks, and to trigger single-node timeouts earlier than intended. While clock skew can induce delays and timeouts in Tendermint, it does not appear to affect safety: we have yet to observe a nonlinearizable outcome in either register or set tests.
3.2 Crash Safety
We evaluate crash-safety by killing Tendermint and Merkleeyes on every node concurrently, then restarting them, every 15 seconds. Connections drop and in-flight transactions will time out, but once restarted, it only takes 5–10 seconds to restore normal operation.
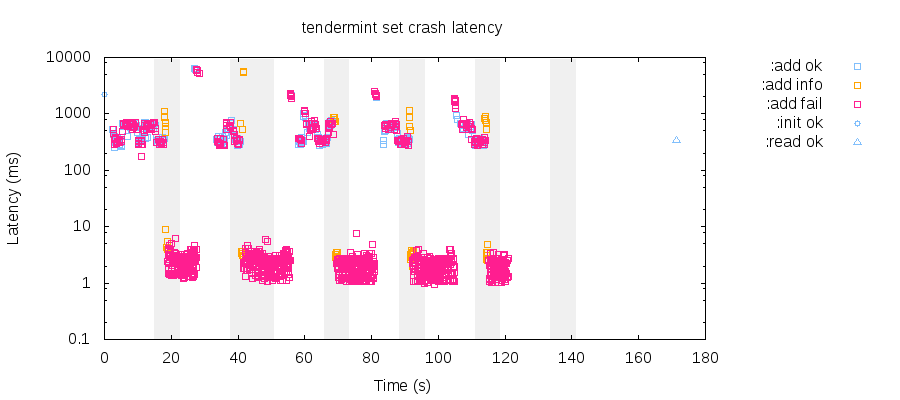
In this plot of a set test’s latencies, shaded regions indicate the window where nodes were crashed. Note that latencies spike to 2–10 seconds initially, then converge on 500-1000 ms once the cluster recovers. Low-latency failures are connection-refused errors. info operations are indeterminate; they may have either succeeded or failed.
3.3 Network Partitions
We evaluated Tendermint safety with several classes of network partitions. We isolate individual nodes; split the cluster cleanly in half; or construct overlapping-ring topologies, where nodes are arranged in a ring, and each node is connected to its nearest neighbors, such that every node can see a majority of the cluster, but no two nodes agree on what that majority is. Although we can induce latency spikes with single-node partitions, and long-lasting downtime by splitting the cluster in half or with majority rings, no network partition resulted in nonlinearizable histories.
3.4 Byzantine Validators
Verifying byzantine safety is, in general, difficult: one must show that malicious validators are unable to compromise safety, which requires that we know (and implement) appropriately pernicious strategies. For time reasons, we have not built our own byzantine Tendermint validators. However, we can test some measure of byzantine fault tolerance by running multiple copies of legal validators with the same validator key, and feeding them different operations. These duplicate validators will fight over which history of blocks they prefer—using their signing key to vote twice for different alternatives, and, hopefully, exposing safety issues.
Unfortunately, these types of byzantine validators do not seem capable of causing nonlinearizable histories—so long as we constrain byzantine validator keys to own less than 1/3 of the total votes. If they own more than 1/3 of the votes, then it is theoretically possible to observe nonlinearizable histories.
For instance, consider a four node cluster: two nodes A and Aʹ with the same validator key, and non-byzantine nodes B and C. Let the key shared by A and Aʹ have 7 votes, and B and C have 2 votes each. The total number of votes in the cluster is therefore 11, and any group of nodes with at least 8 votes controls a 2/3 majority and can commit new blocks. Without loss of generality, if A proposes transaction T and B votes for it, then [A, B] has 9 votes and can legally commit. At the same time, [Aʹ, C] also has 9 votes and can commit a totally independent block, leading to inconsistency.
However, this anomaly is difficult to observe: when a Tendermint node encounters two conflicting blocks which were both signed off on by the same key, that node crashes, and a majority of the cluster quickly comes to a halt.
Clusters with these “super-byzantine” validators tend to kill themselves before we can observe safety violations. We need a more sophisticated approach.
panic: Panicked on a Consensus Failure: +2/3 committed an invalid block:
Wrong Block.Header.LastBlockID. Expected
25D18C27F8E1DC2C0F858D80DDBBE272E1DA9E27:1:567B03A9A6FC, got
EE5BD42D329C8925123AF994FDF25E2D1053D2C8:1:A3D3511E25313.5 Byzantine Validators with Partitions
To observe divergence, we need to keep both components of the network independent from one another long enough for both to commit—for instance, through a particular type of network partition. We use two in the Tendermint Jepsen tests. The first picks one of the duplicate validators to participate in the current cluster, and isolates the others completely, unable to make progress. As duplicate validators swap in and out of the majority component, we simulate a single validator which is willing to go back on its claims—voting differently for the same blocks. This technique can result in nonlinearizable histories, but only when duplicate validator keys control more than 1/3 of the vote.
A second, more robust partition splits the cluster evenly, such that each duplicate validator is in contact with roughly half of the non-byzantine nodes. This approach yields safety violations more reliably, since both components have sufficient votes to perform consensus independently. For instance, in this run, several concurrent set tests report the loss of a handful of transactions:
{:valid? false,
:lost "#{96 110 119..120 122 126}",
:recovered "#{}",
:ok "#{0 3 5 ... 123 125 128}",
:recovered-frac 0,
:unexpected-frac 0,
:unexpected "#{}",
:lost-frac 2/43,
:ok-frac 53/129}However, so long as byzantine validators control less than 1/3 of the vote, Tendermint appears to satisfy its safety claims: histories are linearizable and we do not observe the loss of committed transactions.
3.6 File Truncation
To make the crash-recovery scenario somewhat more aggressive, we introduce a byzantine variant, where write-ahead-logs are truncated during a crash. This simulates the effects of filesystem corruption. We kill Tendermint and Merkleeyes on up to 1/3 of the validators, chop a few random bytes off the Merkleeyes LevelDB logs on those nodes, then restart. Because Tendermint is byzantine fault-tolerant, we should be able to arbitrarily corrupt logs on up to 1/3 of the cluster without problems.
This scenario does not appear to lead to the loss of acknowledged operations, but it can cause Merkleeyes to panic on startup, as the LevelDB recovery process is unable to handle logfile truncation under certain circumstances. If more than 1/3 of the validators experience this type of fault, it could render the cluster unusable until a suitable program can be written to process the LevelDB log files.
We believe this is due to one or more bugs in goleveldb’s recovery code; there have been reports of similar panics in goleveldb from Prometheus and Syncthing, and consequent bugfixes which may address the issue in Tendermint as well. The Tendermint team plans to update goleveldb and see if this addresses the problem.
In addition to Merkleeyes, Tendermint’s consensus system has its own write-ahead log. Unlike Merkleeyes, truncated entries in the Tendermint WAL are silently ignored, and preceding entries are correctly recovered instead of panicking the server.
Because 2/3 of the cluster remains online in our scenario, Tendermint can continue processing transactions throughout the test. However, there is a distinct impact any time a node crashes: that node closes connections and refuses new ones, which results in a stream of low-latency failures in the latency distribution. We also see elevated latencies—on the order of three to four seconds—due to the repeated failure of a single node. Because nodes take turns proposing new blocks in Tendermint, the failure of any single node disrupts the commit process for 1 : n blocks—the remaining nodes must wait for timeout_propose (which defaults to three seconds) until a healthy node can retry the proposal. These elevated latencies persist until the down node recovers, or until it is ejected from the validator set, e.g. by an operator. Note that this is different than a leader-based system like Raft, where the loss of a leader causes every transaction to time out or fail, but once a new leader is elected, latencies return to normal.
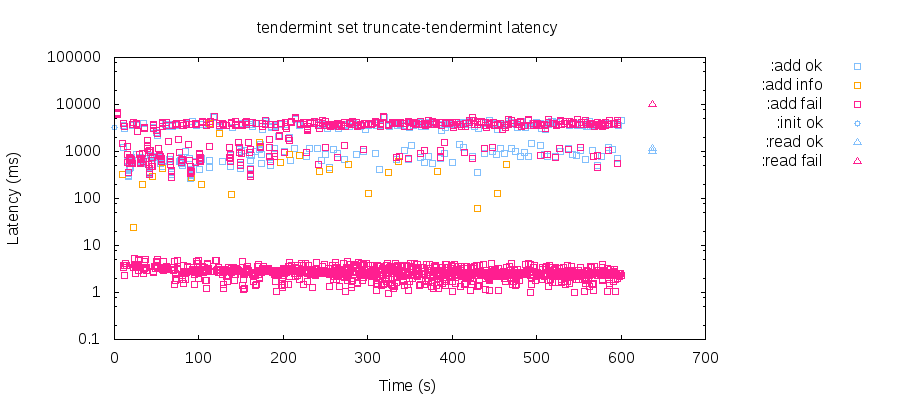
So long as truncation affects less than 1/3 of the cluster, Tendermint appears safe; we have not identified any linearizability violations due to WAL truncation. However, there is a more subtle problem lurking in the Tendermint WAL: it doesn’t fsync operations to disk. When transactions are written to the log, Tendermint calls write (2) before returning, but fails to fsync. This implies that operations acknowledged as durable may be lost if, say, the power fails. Tendermint closes and reopens files regularly, but close (2) doesn’t fsync either. Due to time constraints, we have not experimentally reproduced this behavior, but it seems likely that a simultaneous power failure affecting more than 1/3 of the cluster could cause the loss of committed transactions. Tendermint is working to ensure data is synced to disk before considering it durable.
3.7 Dynamic Reconfiguration
Tendermint supports dynamic cluster membership: a special transaction type allows operators to reweight validator votes, add new validators, or remove existing validators, at runtime. In addition, we can start and stop instances of validators on physical nodes, creating cases where validators are running nowhere, move from node to node, or run on n nodes concurrently: a byzantine case.
We designed a state machine for modeling cluster state, generating randomized transitions, ensuring those transitions result in legal cluster states, and applying those transitions to the cluster. We ensure that 2/3 of the cluster’s voting power remains online, that less than 1/3 of the cluster is down or byzantine, that no more than 2 nodes run validators which are not a part of the cluster config, and that no more than 2 validators in the config are offline at any time.
These rules keep the cluster in a continuously healthy state, which is important because changing the validator set requires that Tendermint is still capable of committing transactions—if we prevent Tendermint from making progress, we won’t be able to continue the test, or, for that matter, change the membership to fix things. Similar constraints prevent us from testing network partitions combined with reconfiguration, at least in general: a partition might prevent the cluster from repairing faulty replicas between transitions, leading to safe states which are, in actuality, unsafe.
With these caveats, we found no evidence of safety violations through hundreds of cluster transitions. Tendermint appears to preserve linearizability, so long as the aforementioned constraints are satisfied.
4 Discussion
We uncovered three durability issues in our research. The first is a crash in Merkleeyes, the example key-value store, where the on-disk store could become corrupt due to repeated updates on a single key. The second is a bug in goleveldb, which causes Merkleeyes to crash when recovering from a truncated logfile. The third is a problem with the Tendermint WAL, which is not synced to disk before operations are acknowledged to clients. If more than 1/3 of the cluster experiences, say, power failure, it might allow the loss of acknowledged operations. All three of these issues are confirmed by the Tendermint team, and patches are under development.
Otherwise, Tendermint appears to satisfy its safety guarantees: transactions appear linearizable in the presence of simple and complex network partitions, clock skew, and synchronized crash-restart cycles. In addition, Tendermint appears to tolerate byzantine faults on less than 1/3 of the cluster, including duplicated validators with or without partitions, dynamic membership changes, and file truncation.
As an experimental validation technique, Jepsen cannot prove correctness; only the existence of bugs. Our experiments are limited by throughput, cluster recovery time, and operation latency; as Tendermint matures and performance improves, we might be able to detect faults more robustly. It is also possible that composite failure modes—for instance, changing the nodes in a validator set during a particular network partition—might prove fruitful, but we have not explored those here.
We have also not formally proved the cryptographic or safety properties of Tendermint’s core algorithm, nor have we model-checked its correctness. Future research could engage formal methods to look for pathological message orders which might lead to safety violations, or cryptographic attacks against the Tendermint consensus algorithm.
This research was funded by the Tendermint team, and conducted in accordance with the Jepsen ethics policy. We would like to thank Tendermint for their assistance in designing these tests, and for developing new Tendermint features to support Jepsen testing.
There exist byzantine fault tolerant consensus algorithms which require only two network delays in the common case, instead of four; for instance, Martin & Alvisi’s Fast Byzantine Paxos.↩
Typical latencies for blockchain systems are on the order of seconds to minutes; ~1 second latencies are relatively quick by comparison.↩
Most Raft implementations are built as language-specific libraries, with an API for plugging in state machine logic. Tendermint differs in that it runs the consensus system and state machine in separate binaries.↩
